Mathematical Interests:
Classes Taken: Topology • Real Analysis • Abstract Algebra • Graph Theory • Linear Algebra • Vector Calculus • Proofs and Fundamentals • Calculus 1 and 2
Interested in Topology, Affine Geometry, Math Visualisation, Analysis
Passion for Designing Math Diagrams, Visuals, and Activities
Image created for my Senior Project at Bard College
Senior Project Research
Stellate neighborhoods from the side and the top.
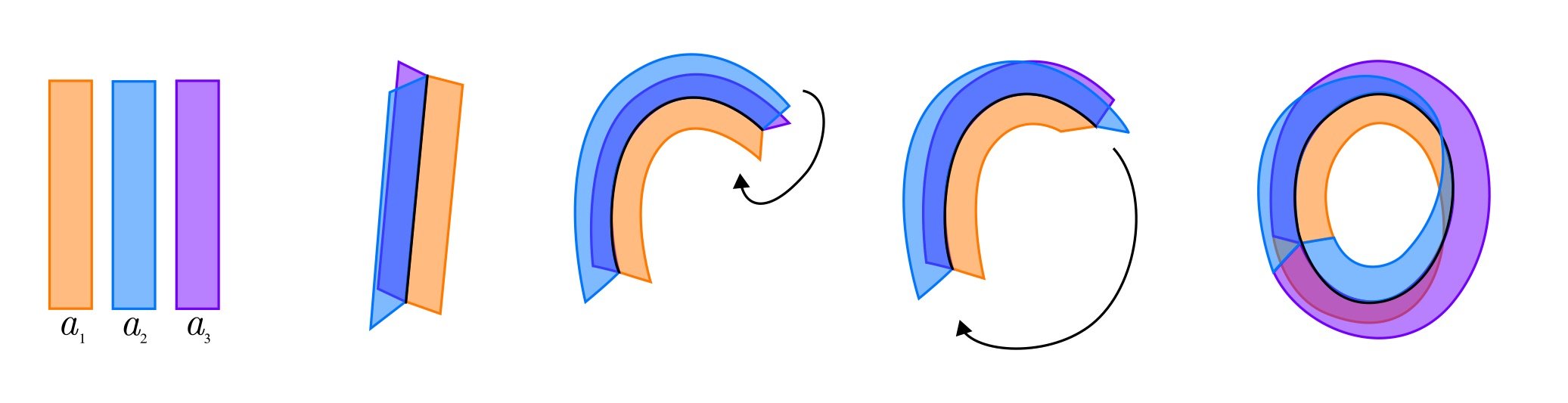
Making a stellate union called a stellate washer.
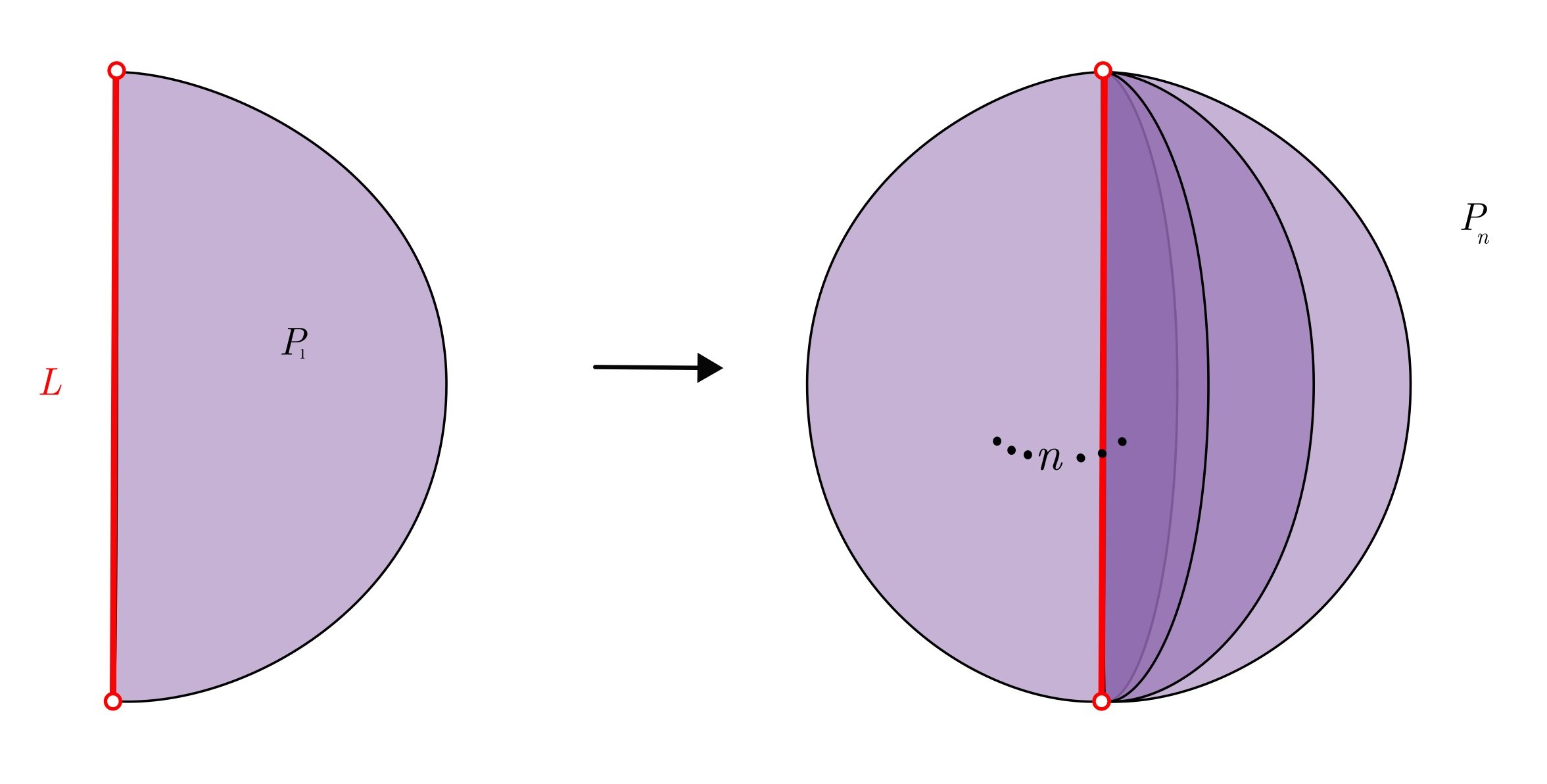
Stellate neighborhoods are created by gluing half disks together along their straight edges.
A 1-stellate neighborhood is a half disk, a 2-stellate neighborhood is a disk, a 3-stellate neighborhood is 3 half disks glued together to make a star-like shape, and so on.
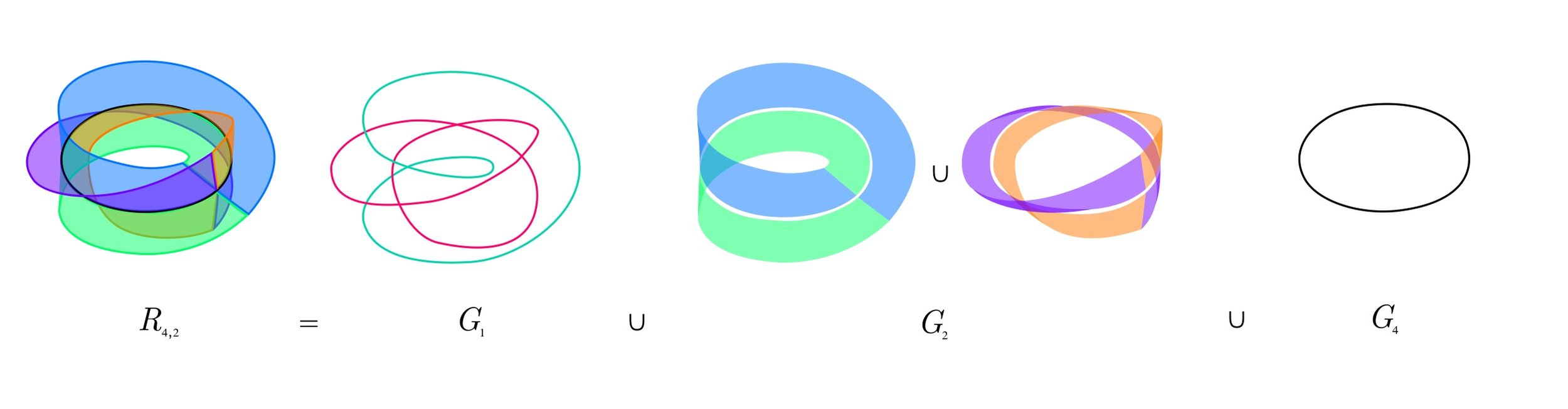
For a topological space $X$, and for each $n \in \nn$, the $n$-stellate subspace of $X$ is the set of all points in $X$ that have $n$-stellate neighborhoods. I will be examining topological spaces called stellate unions, where each point in the space is contained in an $n$-stellate subspace for some $n \in \nn$.
All surfaces and surfaces with boundary are stellate unions, yet there are many stellate unions that are not surfaces or surfaces with boundary.
The ultimate goal of this project is to study various stellate unions and gather useful information using stellate neighborhoods.
A stellate washer broken up into its. stellate subspaces.
Past Research: QUADs
Research conducted with Professor Lauren Rose with the aim to understand the combinatorics behind the game Quads.
Our mission was to count the number of qaps(non-quad) within a k-flat by hand. We are also working on finding different kinds of qaps and researching how these behave.
Started this work in the summer of 2020 through the Bard Summer Research Institute, and have continued the research in the following semesters.
Created all images/diagrams for written works and example quads cards (displayed below).